교점 구하기

ℹ️

2차원 공간 또는 3차원 공간 상에서 교점을 구하는 방법들을 소개합니다.

두 직선 사이의 교점

Javascript에서 두 직선 사이의 교점을 구하는 법

Math.js의 intersect 함수를 사용하면 다음과 같이 두 직선 사이의 교점을 쉽게 구할 수 있습니다.


// 2D
math.intersect([x1, y1], [x2, y2], [x3, y3], [x4, y4]) as number[];

// 3D
math.intersect([x1, y1, z1], [x2, y2, z2], [x3, y3, z3], [x4, y4, z4]) as number[];

2차원 공간 상의 두 직선의 교점 구하는 수학적인 방법

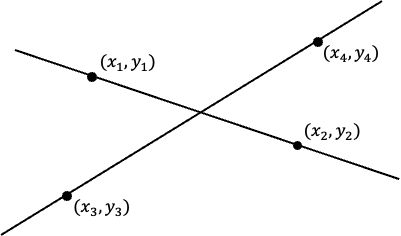
서로 다른 두 점 , 을 지나는 직선 와 서로 다른 두 점 , 를 지나는 직선 가 주어졌을 때, 와 의 교점 는 다음과 같이 구할 수 있습니다.

그리고 의 값이 이면 두 직선의 기울기가 같으므로 두 직선은 평행하거나 일치한다고 볼 수 있습니다.

평면과 직선 사이의 교점

Javascript에서 직선과 평면의 교점을 구하는 법

Math.js의 intersect 함수를 사용하면 다음과 같이 직선과 평면 사이의 교점을 쉽게 구할 수 있습니다.


math.intersect([x1, y1, z1], [x2, y2, z2], [a, b, c, d]);

3차원 공간 상의 평면 방정식

평면 상의 임의의 점 과 평면의 법선 벡터 가 주어졌을 때 평면 방정식은 다음과 같습니다.

수식의 의미를 해석해보면 3차원 공간 상의 임의의 점이 법선 벡터와 수직이면(외적했을 때 값이 0) 모두 평면 상의 점이라고 볼 수 있습니다.

다시 위 식을 일반적인 평면 방정식의 형태로 정리하면,

만약 평면 상의 법선 벡터는 주어지지 않았지만, 평면 상의 서로 다른 임의의 점 3개가 주어졌을 때는 점들을 연결한 두 벡터를 외적하여 법선 벡터를 구하는 방법을 사용하여 평면 방정식을 구할 수 있습니다.

3차원 공간 상의 직선과 평면의 교점 구하는 수학적인 방법

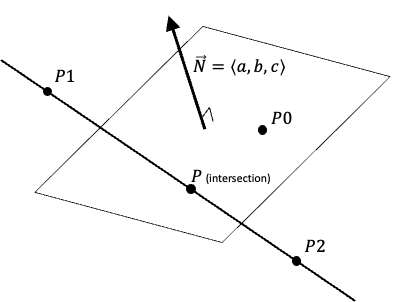
3차원 공간 상에서 점 을 지나고 법선벡터가 인 평면의 방정식은 다음과 같습니다.

서로 다른 두 점 , 를 지나는 직선의 방정식은 다음과 같습니다. (는 직선의 기울기)

직선 방정식을 평면 방정식에 대입하면,

위 식을 에 대하여 전개하면,

마지막으로 를 직선 방정식에 대입하면 교점 를 구할 수 있습니다.

의 활용

의 분모가 인 경우, 평면의 법선 벡터 과 직선이 수직이라는 뜻입니다.

의 값이 이면 교점 는 과 사이에 있다는 뜻입니다.

직선과 삼각형 사이의 교점[1]

C#에서 직선과 삼각형 사이의 교점을 구하는 법

삼각형의 세 꼭지점을 전부 지나는 평면과 직선 사이의 교점이 주어졌을 때, 교점을 구하는 코드는 다음과 같습니다. 아래 코드는 C#이지만 조금 수정하면 다른 언어에서도 쉽게 사용할 수 있습니다.


// ref: Dan sunday, "Intersection of a Ray/Segment with a Plane", Geometry Algorithms,
//      http://geomalgorithms.com/a06-_intersect-2.html
/// <summary>
/// 주어진 좌표가 삼각형에 속하는지 검사한다.
/// </summary>
/// <param name="p0"> 삼각형의 정점 중 하나의 좌표 </param>
/// <param name="p1"> 삼각형의 정점 중 하나의 좌표 </param>
/// <param name="p2"> 삼각형의 정점 중 하나의 좌표 </param>
/// <param name="pi"> 삼각형에 속하는지 검사할 좌표 </param>
/// <returns> 삼각형에 속하면 true, 아니면 false </returns>
public static bool IsPointIn(Vector3 p0, Vector3 p1, Vector3 p2, Vector3 pi)
{
    var u = p0 - p1;
    var v = p2 - p1;
    var w = pi - p1;
    
    var uv = Vector3.Dot(u, v);
    var wv = Vector3.Dot(w, v);
    var vv = Vector3.Dot(v, v);
    var wu = Vector3.Dot(w, u);
    var uu = Vector3.Dot(u, u);

    var si = ((uv * wv) - (vv * wu)) / ((uv * uv) - (uu * vv));
    var ti = ((uv * wu) - (uu * wv)) / ((uv * uv) - (uu * vv));

    return (si >= 0 && ti >= 0 && (si + ti) <= 1);
}

수학적으로 삼각형을 나타내는 방법

삼각형의 세 꼭지점의 좌표 , , 가 주어졌을 때, 이 꼭지점들을 바탕으로 평면의 매개적 방정식을 다음과 같이 나타낼 수 있습니다.

와 는 실수이며, , 은 삼각형의 변벡터(edge vector)입니다.

참고로 삼각형의 세 꼭지점을 평면의 매개적 방정식으로 나타내면 다음과 같습니다.

직선과 삼각형 사이의 교점을 구하는 방법

직선과 평면 사이의 교점 와 매개적으로 표현한 평면의 관계는 다음과 같이 나타낼 수 있습니다.

삼각형은 로 나타낼 수 있습니다. 즉, 평면 상의 임의 점들 중에서 , , 을 모두 만족하는 점들은 모두 삼각형에 속합니다. 와 가 위의 삼각형의 조건을 만족하면 직선과 삼각형은 교차하며, 교점은 가 됩니다.

Hill의 “perp dot product”를 기반으로 bycentric coordinate를 계산하면 와 를 구할 수 있고, 결과적으로 평면과 직선의 교점이 삼각형에 포함되는지 검사할 수 있습니다. 실제 구현 방법은 위의 소스코드를 참고해주세요.

[1] Daniel Sunday, “Practical Geometry Algorithms”, 2021.